Stoic Macro: The Mathematics of Progress
Why Your Learning Has Derivatives
This is the first in a three-part series on a philosophy we call "Stoic Macro"—a framework for navigating uncertainty in both investing and life.
Fair warning: Today's post gets deep into the mathematical weeds. If derivatives make your eyes glaze over, skip to the takeaways at the end, or just wait for tomorrow's post where we'll translate this into practical wisdom.
The Series:
Today: The Mathematics of Progress (theory)
Tomorrow: Living Between Order and Chaos (philosophy)
Day 3: Portfolio Consciousness (practice)
Marcus Aurelius and Buddha arrived at the same truth from different paths: life inherently involves pain. It's not a bug—it's a feature. The Stoics built a philosophy around accepting this reality. The Buddhists made it their First Noble Truth.
But acceptance isn't enough. We need to operationalize this insight.
Ray Dalio gave us the formula:
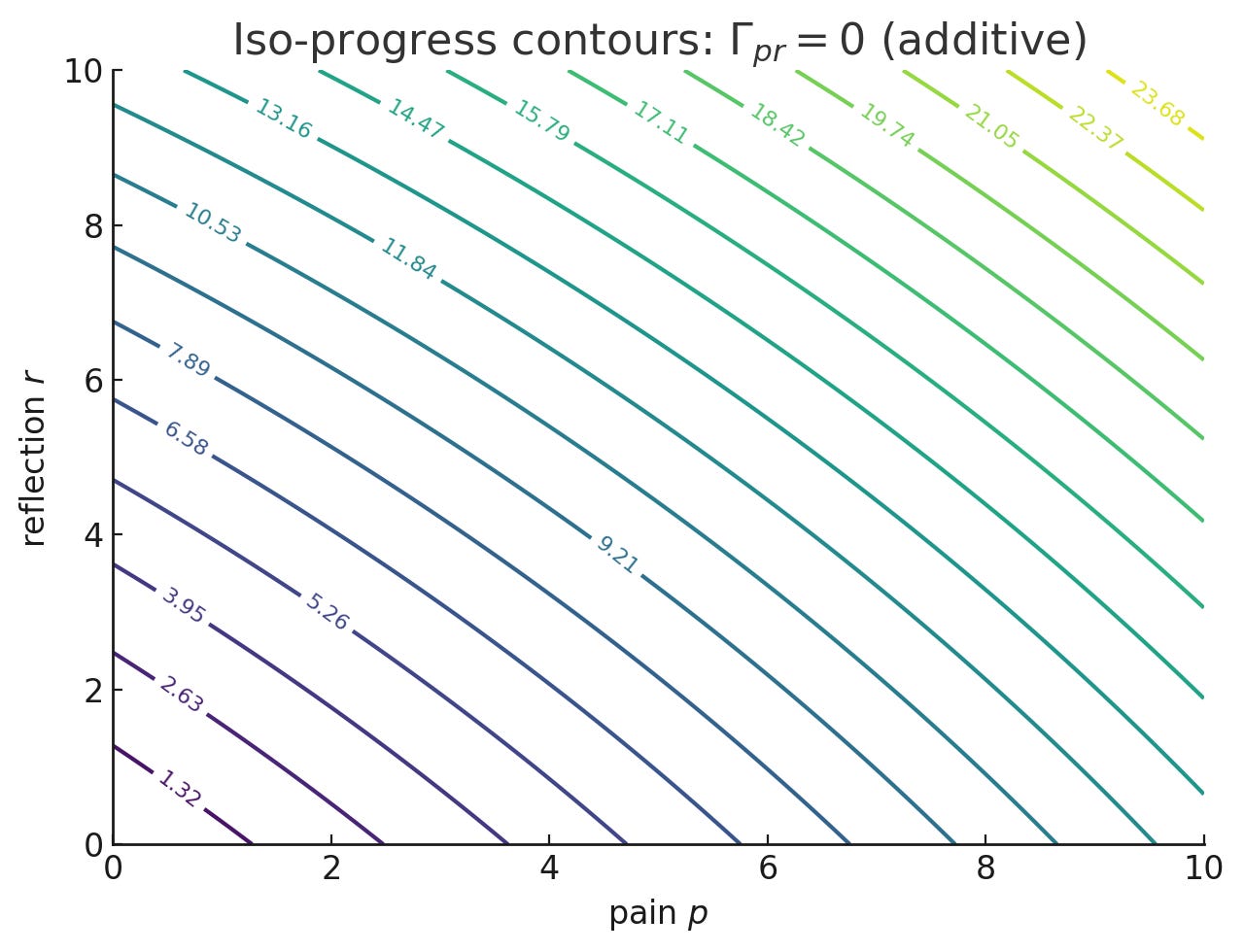
Pain + Reflection = Progress
This equation, being a timeless and universal truth, invites some mathematical exploration. What happens when we treat this not as a motivational poster but as a differential equation we can optimize?
(If you're still reading, you're either a quant or a masochist. Either way, let's begin..)
First-Order: The Speed of Learning
In particular, by realizing that if we think about progress as distance, we can think of it as our speed multiplied by time. Which, once plugged into the above and solving for speed, yields some interesting first order conclusions.
Let's be precise with the math:
where p(t) is cumulative pain experienced and r(t) is cumulative reflection applied by time t.
If we identify progress with distance traveled:
Then average speed (velocity) over time is:
If your goal is progress, and your life is finite (which Bryan Johnson notwithstanding appears true for all mortals), your lifetime cumulative progress towards your goals will be defined by two interesting terms:
p/t= the rate at which you can experience pain
r/t = the rate at which you can reflect on that pain
In essence, the formula for learning.
Second-Order: The Acceleration of Growth
Taking this math a step further (as we are wont to do), and thinking about not just speed but acceleration—the rate of change of your speed, the amount of 'convexity' in your learning engine—reveals something profound.
When we differentiate our speed equation:
This can be rewritten more intuitively as:
Each term is (instantaneous rate − average rate) ÷ time.
What This Means
If we think of p(t)/t as your capacity for pain (historical average pain per unit time), then:
It says something pretty interesting. If you assume that over time, we become acculturated to a given level of pain, your rate of change of your capacity is defined by a simple term:
How much pain you are experiencing now compared to your historic capacity
Meaning if you aren't experiencing pain, acutely, in the moment, you aren't growing. If you aren't pushing yourself to reflect deeper than you have before, you are atrophying.
A shark that isn't swimming is a dead shark.
The Convexity Engine: Cross-Derivatives
This gives us the derivatives of learning. But to really understand the dynamics, we need to examine the second-order effects more carefully. Let progress be a response surface:
The "gammas" (second derivatives) are:
Pain Gamma:
Do additional units of pain keep teaching you more?
Γpp>0 means antifragility to adversity—each additional challenge yields increasing returns.
Reflection Gamma:
Do later hours of reflection produce more per hour than your first?
Γrr>0 means meta-learning compounds.
Cross Gamma (the most fascinating):
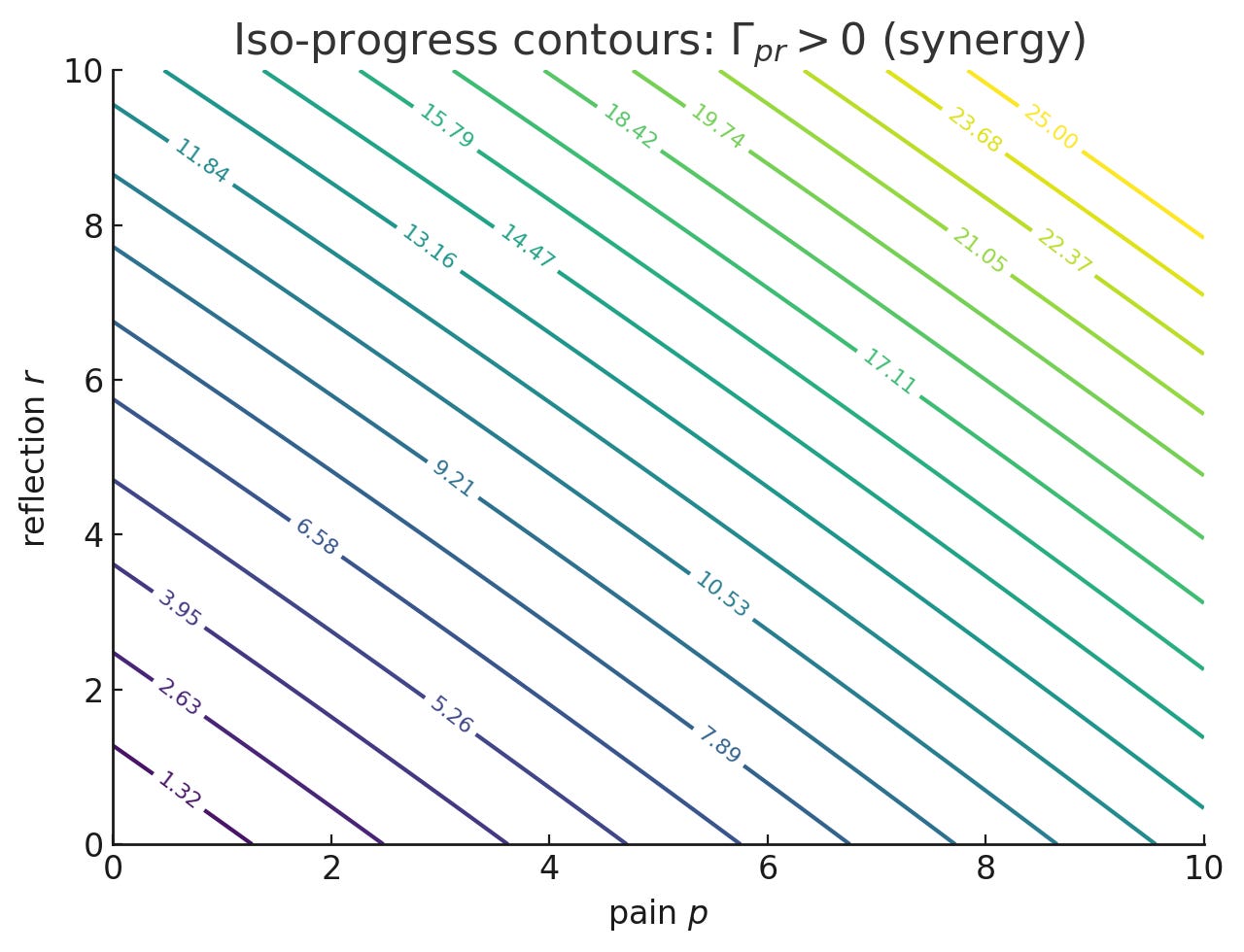
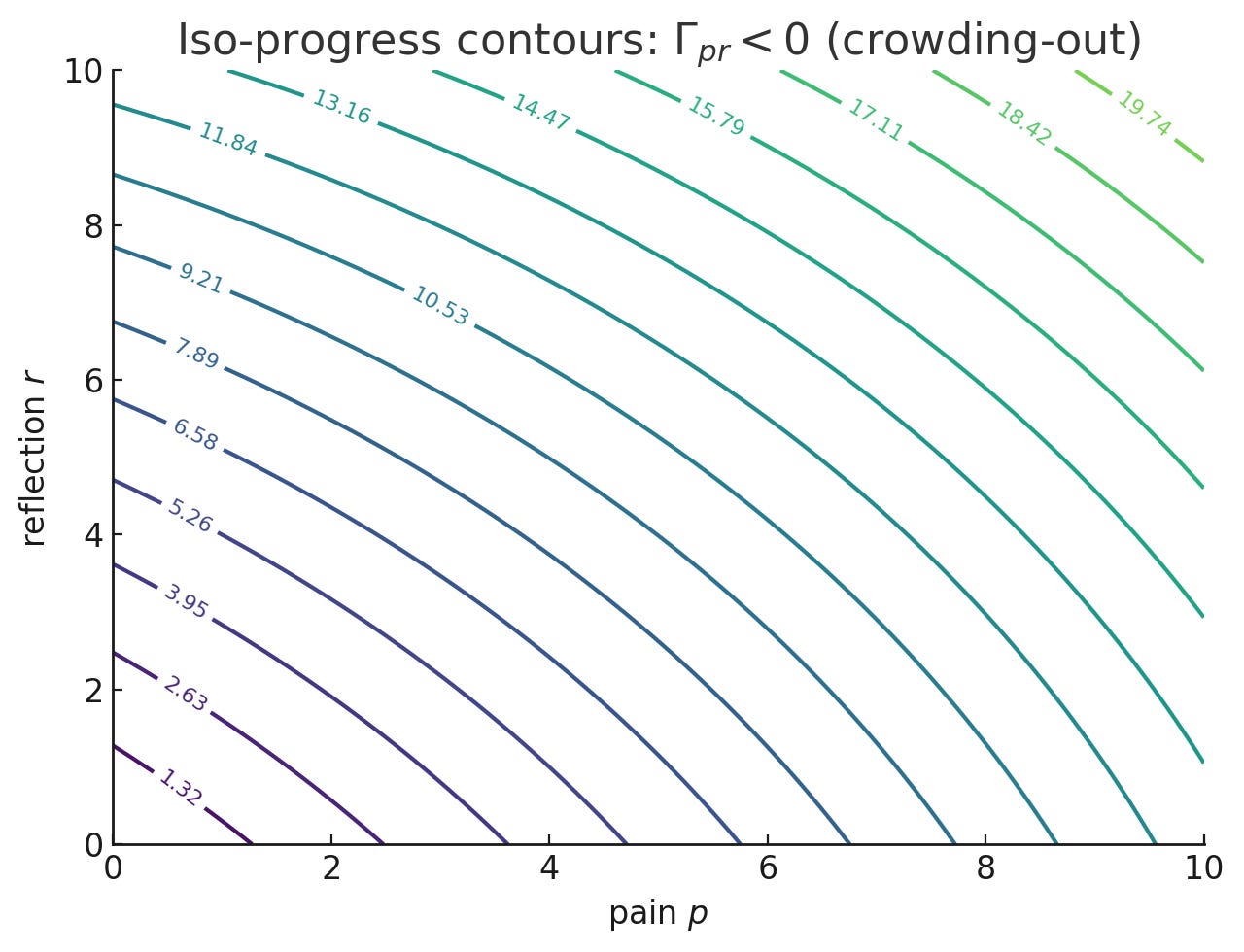
This cross-derivative captures synergy between pain and reflection:
Γpr>0: Complements—more reflection raises the marginal value of pain, and vice versa
Γpr=0: Additive—no interaction effects
Γpr<0: Substitutes—they crowd each other out
Where It Shows Up Dynamically
In the instantaneous acceleration equation:
The highlighted interaction term 2fprp˙r is strictly positive when:
fpr>0 (positive cross gamma)
Both p˙,r˙>0 (you're actively experiencing pain AND reflecting)
Fresh pain combined with immediate reflection creates explosive learning speed, but only if you can maintain both terms over time.
Decay and Time Dynamics
But there's a critical factor: decay. Both pain and reflection fade over time:
Pain decay rate (λp): How quickly lessons from adversity fade from memory
Reflection decay rate (λr): How quickly insights become stale or forgotten
Your effective speed becomes:
High decay rates destroy convexity. The key is building systems that preserve lessons—what I call "reflection infrastructure." If you just write off pain, if you don’t linger on your reflections, you will never be convex in building your capacity for pain and reflection. Think Navy Seal’s after action reviews or trader post-mortems.
Takeaways
To maximize your learning convexity:
Raise first-order rates: Increase p˙ via hard challenges; increase r˙ via deliberate review
Engineer positive cross-gamma: Design challenges and reflection loops where pain and reflection amplify each other
Cut decay rates: Externalize memory (notes, checklists, post-mortems) to lower λ
Time the coupling: Pair each high-pain episode with tightly timed, structured reflection to harvest the 2Γprp˙r˙ term
Next time we will operationalize this philosophical framework, followed by deploying this into the practical world of macro investing (hence “Stoic Macro”). For now, remember: if you're not experiencing acute pain relative to your historic capacity, you're not growing.
The math doesn't lie.
Disclaimers



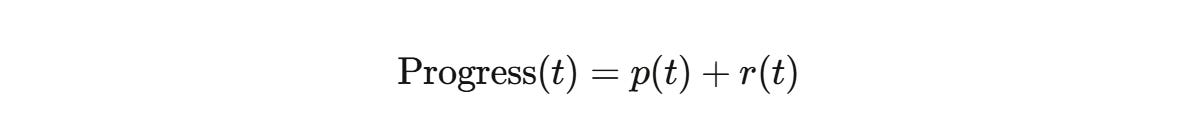
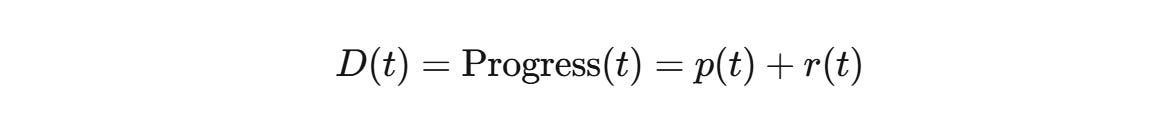
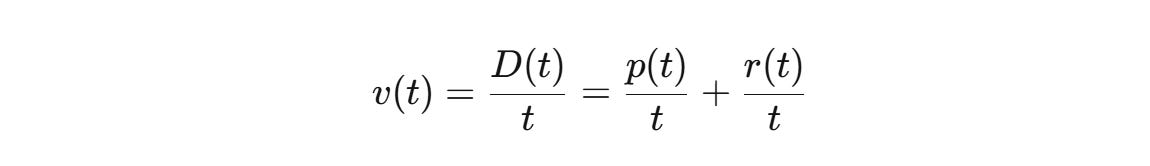
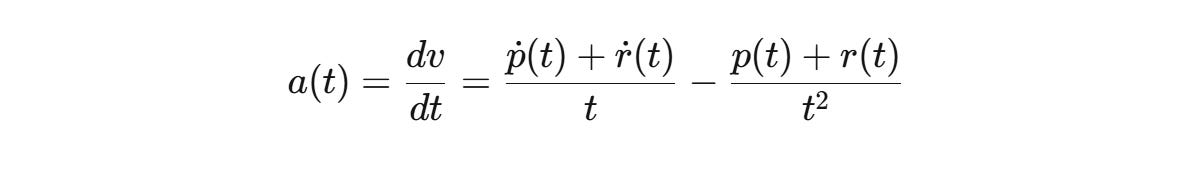

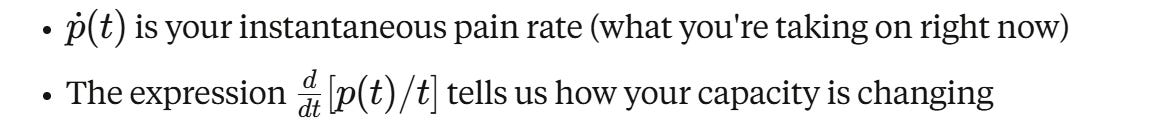

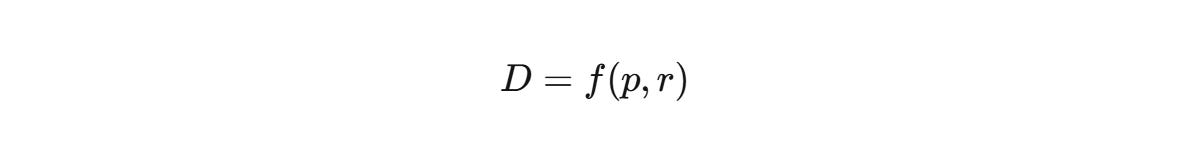
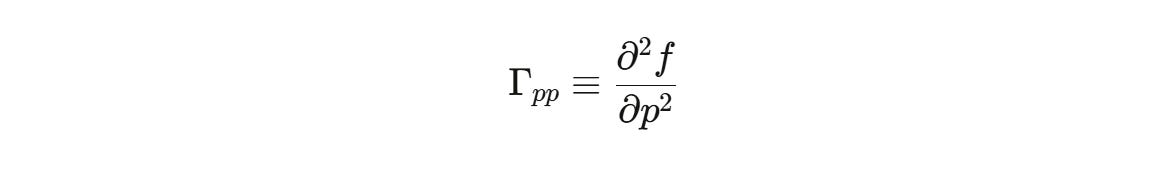




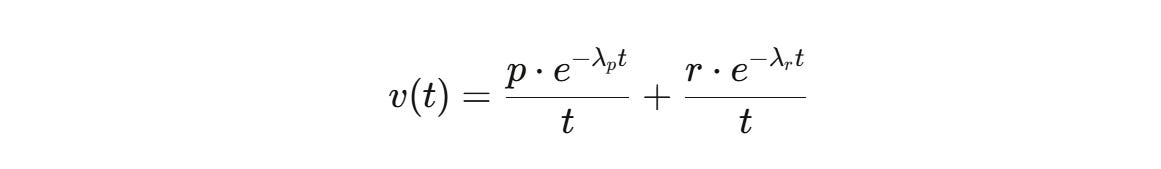
This was all excellent.
Anything that numbs pain (eg alchohol ) should be deleted.
Anything that delays/hinders reflection process.
Intriguing, look forward to the next post. It makes me wonder: 1. Mental vs physical pain and progress, similarities and differences? Conceptually would seem to be similar - after all mental is ultimately physical too. 2. Productive vs unproductive pain - presumably unproductive pain is just pain without reflection and therefore no progress. Will wait to see what the next post says about this if anything.